おわんの底よりも低位に下がることができてかつ、おわんの底以外に臨界点がない地形は存在するか?
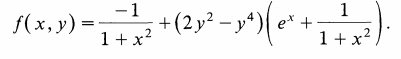
院試の採点中に他の教員の方から質問されて即答できなかった「極小値をもつが最小値ではなく、他に極値を持たない函数」の例。この例では原点は唯一の臨界点で、極小であるが平面全体で最小ではないhttp://www.maa.org/sites/default/files/J00830._Marshall_Ash_and_Harlan_Sexton.pdf …pic.twitter.com/PcQW1hHVKz
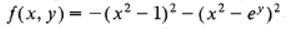
似たような反例として「二変数函数で二つのみ極大点をもつが、他に臨界点を持たない函数」 http://www.jstor.org/stable/2690137?seq=10 …二つ山があれば間に峠点なり極小点が必ずあると思われるが実はそうではない。グラフを描いても見にくいpic.twitter.com/QESFWKJVeR
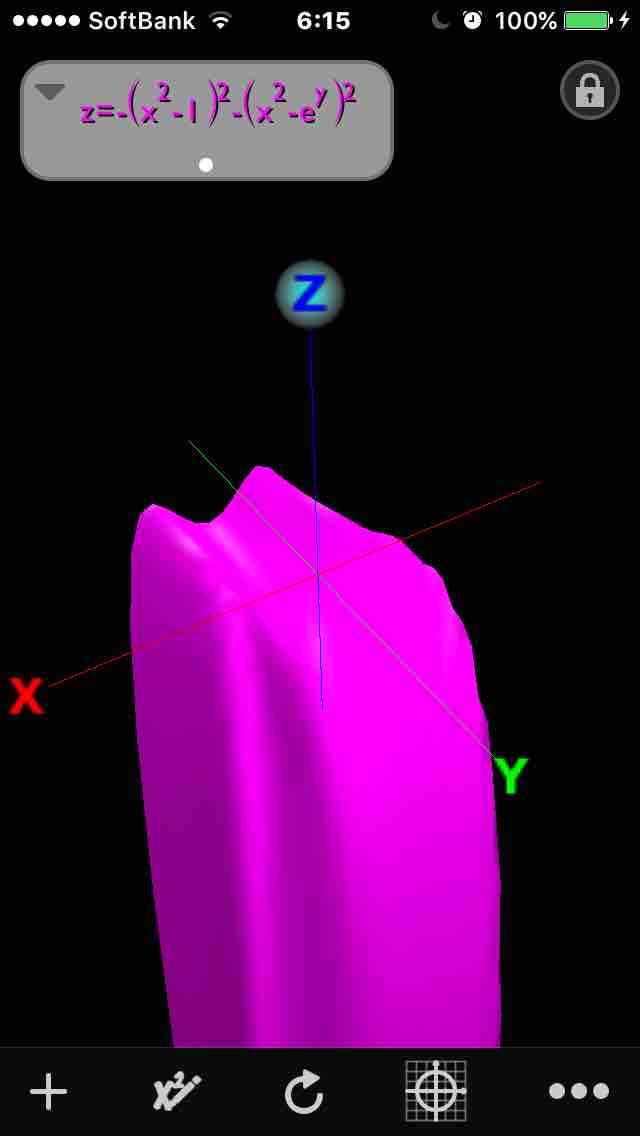
jstorの論文は登録すれば無料で読める。この二つ山があって峠のない函数のグラフはwolfram alphaでみてもよくわからないhttps://www.wolframalpha.com/input/?i=-(x%5E2+-+1)^2+-+(x^2+y+-+E^y)^2 …
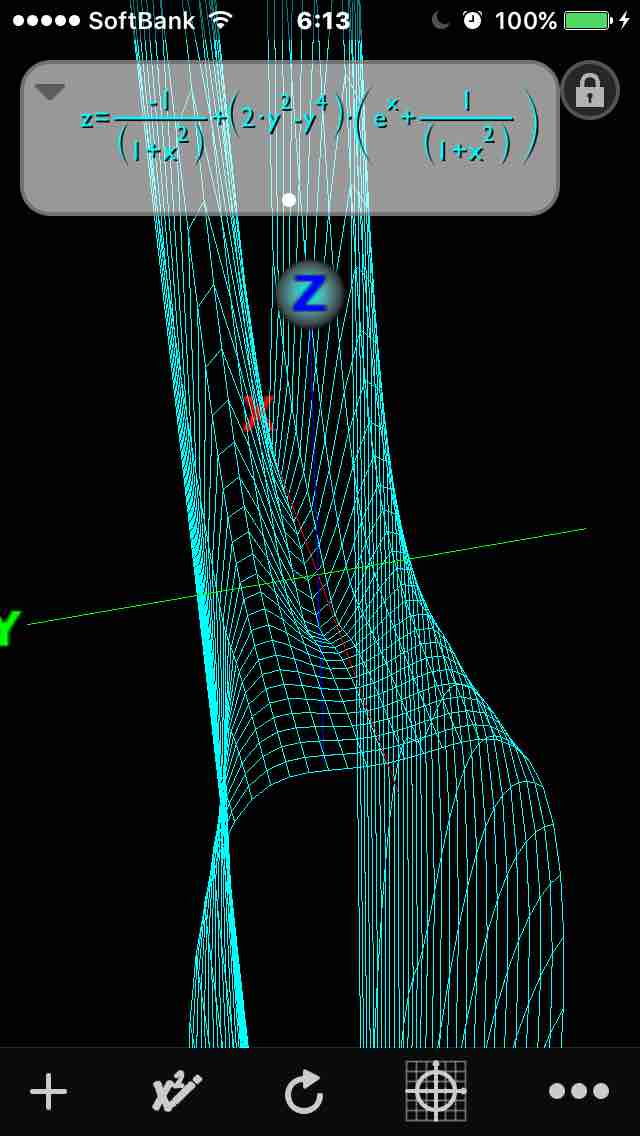
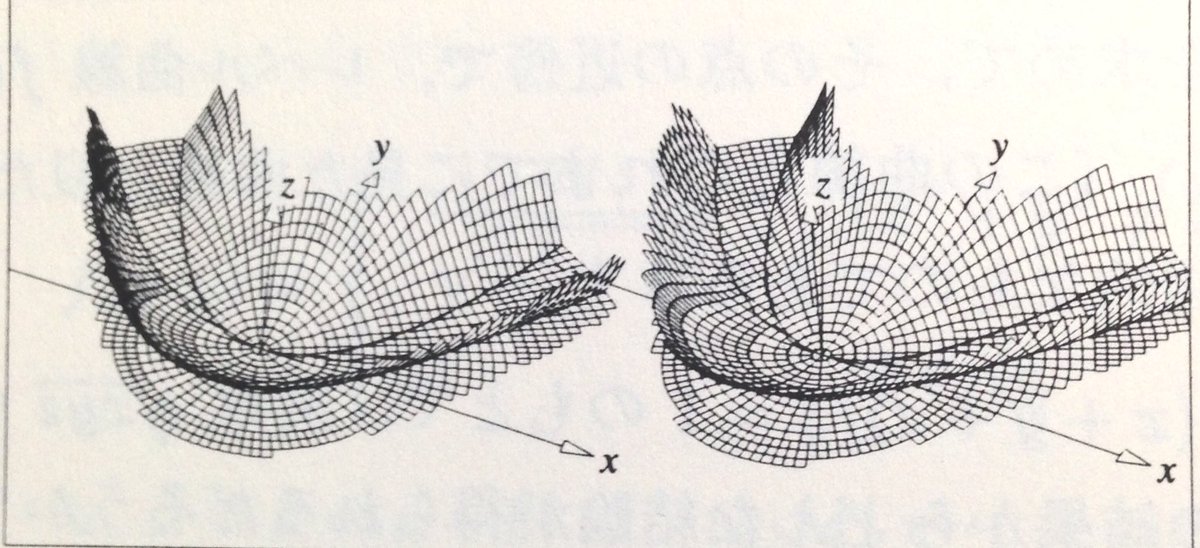
#数楽 https://twitter.com/Paul_Painleve/status/768486207797862400 …iPhoneのQuick Graphというアプリでグラフを書いてみました。もう一枚に続くpic.twitter.com/lA6qd081S0

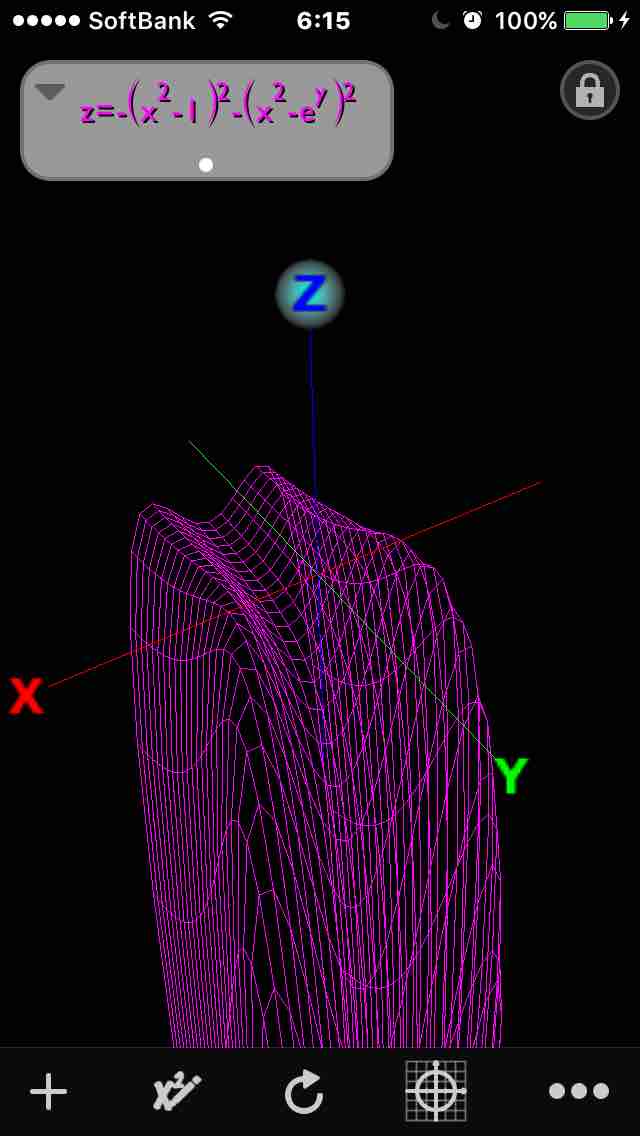
#数楽https://twitter.com/Paul_Painleve/status/768502634529497089 …こちらについてもiPhoneのQuick Graphでグラフを描いてみた。もう一枚に続く。pic.twitter.com/P0ghXB6kYX
#数楽 もっと高級なことをできる道具も手もとにありますが、式を入れるだけでグラフを描いたり、様々な計算を教えてくれたりするツールは便利だよね。先のQuick Graphとか、WolframAlphaとか。中学生あたりから使い始めるといいと思う。
昨夜のツイートにファボが多かったのと訂正も受けたので、少し解説をかねて長く書きます。多変数函数f(x1,x2,,,,,xn)で偏微分が全て0になる点を「臨界点」と呼びます。函数が極大・極小になるなら臨界点になるが、逆は成り立たない。以下、微分可能性は十分あると仮定します。

#数楽https://twitter.com/Paul_Painleve/status/768486207797862400 …「極小値をもつが最小値ではなく、他に極値を持たない函数」の例。yを固定しながらグラフを描いた。yは赤0→橙0.5→黄1→緑1.3→空1.4→青1.42pic.twitter.com/EmqueOXuvd
1変数であれば、ある区間(a,b)で定義された微分可能な函数がただ一つの極小値を持ち他に臨界点を持たなければ、自動的に最小値になります。1変数でも不連続にすれば反例はあります https://twitter.com/tactn001/status/768551136697589760 … … が、さすがに定義域は連結で考えたい。
#数楽 z=f(x,0)はx=0で最小。yを大きくして行くとz=f(x,y)はxの函数として単調増加函数になる。そこからさらにyを大きくするとf(x,y)はyの函数として単調減少。x軸方向とy軸方向の少なくともどちらかで傾きがゼロでなくするようにしてある。
そこで2変数ではどうなるか。問題設定としては「平面全体で定義され、臨界点が一つしかなくそこで極小ならその極小値は大域的にも最小か?」 感覚的には反例がありそうだけど、他に極大・峠点をもたないように作るのは工夫がいるというのがhttps://twitter.com/Paul_Painleve/status/768486207797862400 …
#数楽 おわんの底から出ておわんの底よりも低位に下がれる地形をおわんの底以外に臨界点がなくなるように作る問題。おわんの底から出て下に降れる場所が勾配のある尾根にあれば臨界点を作らずに無限に降れる。ふう。個人的にはこれですっきりした感じ。
.@NoMore_JILPT 訂正ありがとうございます https://twitter.com/NoMore_JILPT/status/768523655802302465 …また先ほどの,@tactn001さんのx^3+y^3-3 x yも(1,1)で唯一の極小点ですが原点に峠点を持ちます
臨界点を他にもっていいのなら、一変数でも3次函数 x-3- 3xは極大・極小はそれぞれ一つずつだけど最大・最小にはならない。2変数なら、極小が一つで極大がなくても峠点があれば、うまくかわして最小にならないようにできる。この峠点を「無限大にうまく飛ばす」ことで反例が作れます
(符号を変えて) 3xy - x^3 - y^3 の峠点である原点を無限遠にとばすにはyをe^y に変えて、3 x* e^y-x^3-e^(3 y)とすれば良いという簡単な解説:http://www.maa.org/sites/default/files/Ira_Rosenholtz_and_Lowell_Smylie33701.pdf …
Ira Rosenholtzさんはこんな例をよく考えているようで、似た話としてもう一つ紹介したのが「極大点を二つだけもつが他に臨界点を持たない」函数。二つ山があれば必ず間に峠がきそうだけど、2変数ならうまく勾配をつければ峠を消せるhttps://twitter.com/Paul_Painleve/status/768502634529497089 …
ただ一つの臨界点を持ち、そこでは極小になるが大域的には最小値ではない2変数多項式の例としてはx^2+(1+x)^3 y^2があります。またこのような性質を持つ4次以下の2変数多項式は存在しないようです。
野村隆昭著『微分積分学講義』で知りました。
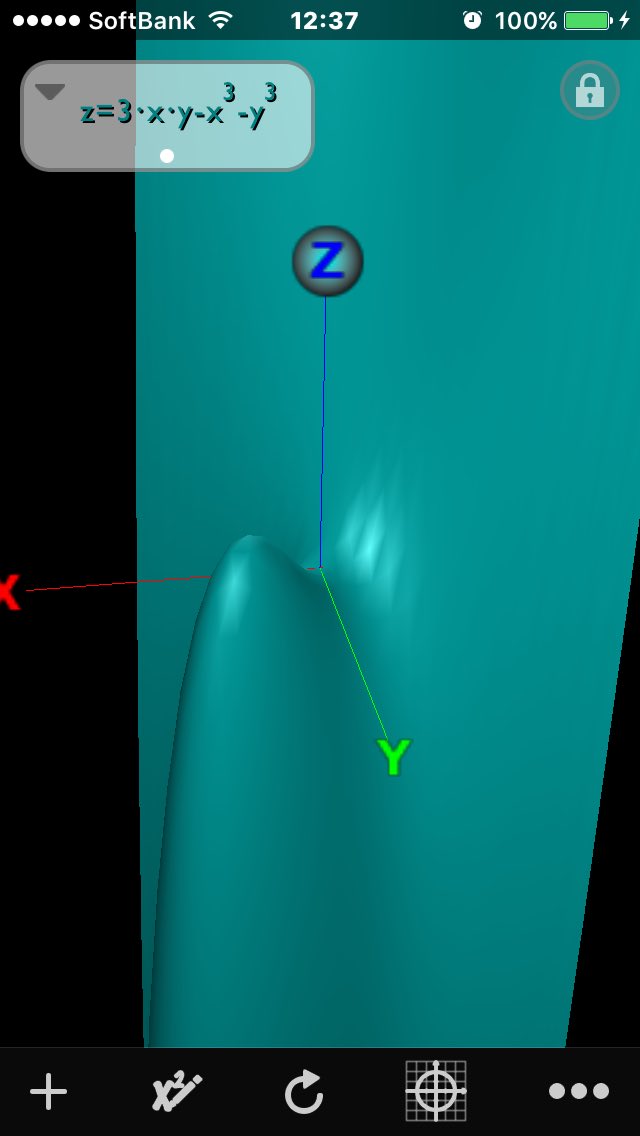
#数楽 https://twitter.com/paul_painleve/status/768597370443403264 …この例もグラフを見たい人がいると思ったのでつくりました。z=3xy-x^3-y^3 の原点は臨界点(峠点)pic.twitter.com/Sb5C8TePBw

#数楽 私がいつもiPhoneで使っているQuick GraphKZ Labs「Quick Graph: Your Scientific Graphing Calculator」https://appsto.re/jp/pVDBr.i
#数楽 iPhoneで購入してほとんど毎日何かに使っているWolframAlphaのアプリWolfram Group LLC「WolframAlpha」https://appsto.re/jp/lF49t.i 保護者は子にねだられたとき、このアプリは買ってあげるべき。
#数楽 WolframAlphaのアプリは有料だが、ウェブで使えば無料でも使える。http://www.wolframalpha.com しかし無料での使用はCPUの制限がきついので、アプリにお金を少し払っておいた方がストレス無く使えるし、数学記号も入力しやすい。
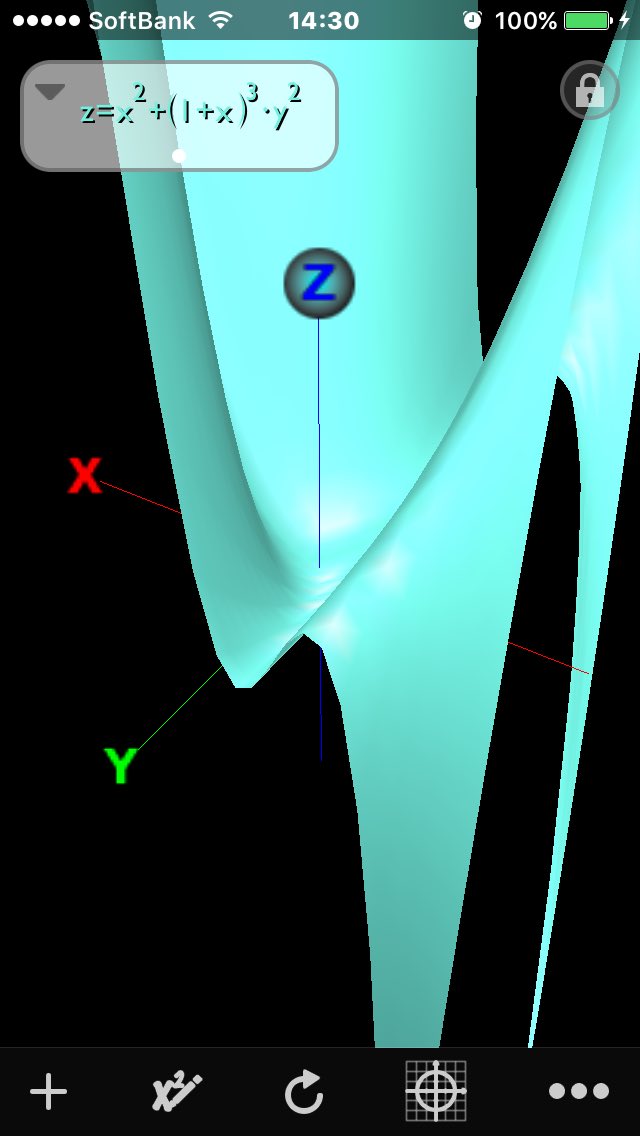
#数楽 https://twitter.com/ryoonosuke/status/768680602648219648 …【ただ一つの臨界点を持ち、そこでは極小になるが大域的には最小値ではない2変数多項式の例としてはx^2+(1+x)^3 y^2があります】Quick Graphでのグラフpic.twitter.com/FzAQCL5keU

#数楽 極小点の原点より下に降りるためには勾配がついている尾根を越えればよい。勾配のついた尾根上には臨界点はない。勾配のついた尾根や谷を使えば臨界点を避けられるという話みたいですね。pic.twitter.com/FzAQCL5keU
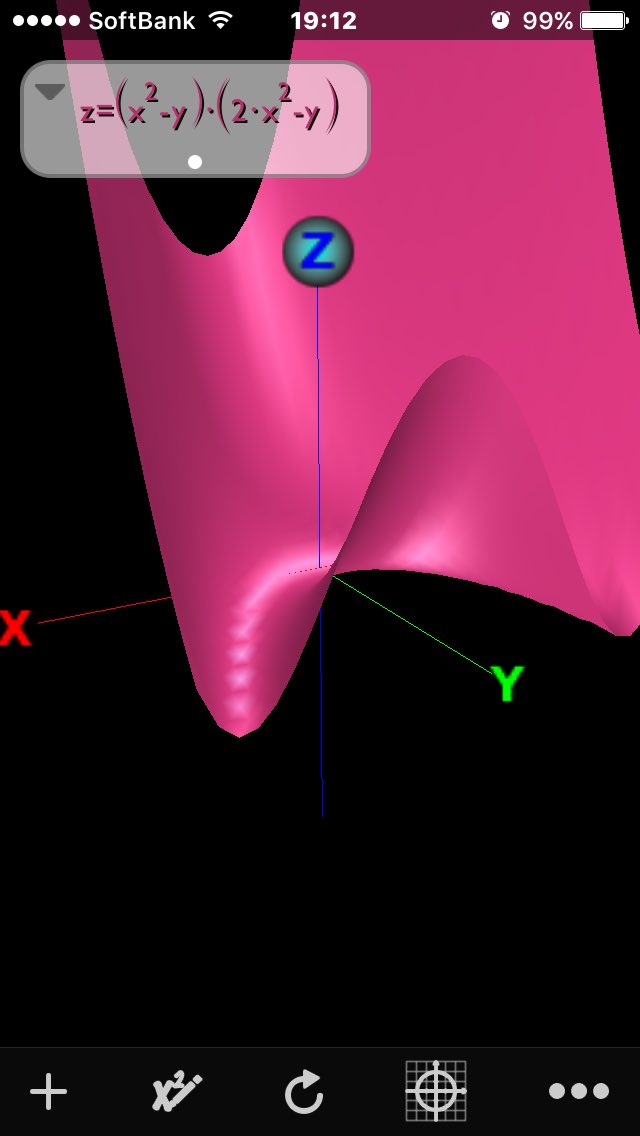
#数楽 https://twitter.com/Paul_Painleve/status/768733559997632512 …z=(x^2-y)(2x^2-y) のグラフ。U字型の谷。原点は谷の中で標高が最も高い。pic.twitter.com/hIufqsHgoe

#数楽 ハイラー&ワナー『解析教程 下』 https://www.amazon.co.jp/dp/4431707514 のp.225より。ペアノさんは若いときに偉い人の数学的誤りを指摘して「誰からも好意を持たれなかった」。ペアノ、いいやつだな(笑)。pic.twitter.com/RGvwt304nq
#数楽 続き。添付画像はその次のページにある立体視。『解析教程』は数学教育用の例を引いてくるためにめちゃくちゃ便利な本。pic.twitter.com/w8rgSKhJcE



